Financial Fraud vs. Election Fraud: Similarities, Differences, and Security

• Actual or not, fraud is widely perceived to have affected the 2020 Presidential election in the United States
• Bank fraud and election fraud have relevant similarities
• Banking cybersecurity techniques are applicable to election security
• Expensivity’s proposal for a Cryptosecure Election Protocol (CEP) would secure the electoral process

With 2020 delivering perhaps the most contentious presidential election in U.S. history, and with charges of fraud in that election widely publicized, it seems timely for Expensivity.com, primarily a money and business website, to offer this article comparing financial and election fraud. There are similarities as well as differences between the two types of fraud, and as stakeholders in both financial markets and representative government, we do well to have some working knowledge of both.

Of primary interest in this article will be the role of digital technologies in advancing, as well as undermining, financial and election security. The final section of this article is by far the longest and most important. It outlines a Cryptosecure Election Protocol that, with only modest digital resources, can guarantee election security. An accompanying slide visualization of the protocol is titled “How a Crypto Protocol Can Ensure Free and Fair Elections.”

1. A Common Framework

In examining financial and election fraud, let’s start with two simplifying assumptions. First, let’s omit financial fraud in which an accountant or financial officer misrepresents the health of a company, such as by valuing it inappropriately or hiding certain liabilities. This is the sort of financial or accounting fraud of which Enron was guilty, but it won’t be addressed here. Second, let’s ignore elections in which the votes of different voters carry different weights, such as where votes at a company board meeting are weighted in proportion to ownership stake. In this article, votes are always whole numbers and one qualified person gets exactly one vote.

Given these two assumptions, our focus then turns to two parties, A and B, or as we’ll call them, Alice and Bob. Alice and Bob can reside in two contexts, a financial context or an electoral context. In a financial context we may refer to financial Alice and financial Bob. Correspondingly, in an electoral context we may refer to electoral Alice and electoral Bob. When the context is clear or when both contexts apply, we’ll usually just refer to Alice and Bob.

In either context, Alice and Bob have a ledger. In a financial context, Alice’s ledger indicates dollar amounts that have been added and subtracted over time (with dates and times of the additions and subtractions), as well as a current total dollar amount of how much she owns (or, if negative, how much she is overdrawn), Similarly for Bob. We can think of Alice’s and Bob’s financial ledgers as their respective bank accounts at a bank, with the ledgers being the records that the bank keeps of credits and debits. For simplicity (as well as to address the possibility of bank fraud), let’s assume that Alice and Bob each have have exactly one account at the same bank. Let’s also assume that each account starts with zero dollars in it, which is in fact how all bank accounts start.

In an electoral context, we think of Alice and Bob as candidates running against each other for the same office. Alice’s ledger indicates votes that have been added or subtracted over time (with dates and times of the additions and subtractions), as well as her current vote total. Similarly for Bob. The vote total in each ledger starts at zero and can never drop below zero. If only legitimate votes are added to Alice’s ledger, there should be no need for votes ever to be subtracted from her ledger. But if there are mistakes and the mistakes are confirmed, then votes can be subtracted, either by invalidating the votes so that neither Alice nor Bob sees their benefit, or by transferring them to the other candidate because they were misassigned. It is the job of the election commission to secure, maintain, and update Alice’s and Bob’s ledger. The election commission for electoral Alice and Bob therefore corresponds to the bank for financial Alice and Bob.

In both the financial and the electoral context, there exists what may be called a true state of affairs. Financial Alice, for instance, after she started her bank account, has deposited funds in and disbursed funds from that account. Leaving aside attempted deposits from other accounts with insufficient funds (which therefore never got deposited with Alice) and disbursements that would overdraw her account (which therefore never got withdrawn from Alice — let’s assume no overdraft protection), the total amount of money in her account is and can only equate to one value. That value will correspond to a true state of affairs, and any other value will not, indicating accounting errors and/or fraud. Ditto for financial Bob.

Electoral Alice likewise has a total amount of votes that should be credited to her. Given all the registered voters in a position to vote for Alice and Bob, some of those will have cast votes for Alice. Those ballots that have been unambiguously filled out in favor of Alice and that have been submitted to the election commission with proper proof of identity from registered voters deserve to counted in Alice’s ledger. These are the total amount of votes to her credit and they can equate to only one value. That value will correspond to a true state of affairs, and any other value will not, indicating vote-counting errors and/or fraud. Ditto for electoral Bob.

The parallelism in these financial and electoral contexts is therefore evident. Sure, there are some crucial differences, which we’ll consider in the next section. But both contexts come down to an accounting problem, keeping track of money or votes over time. One further parallel in keeping with this accounting perspective is, in either context, the irrelevance of intention to the true state of affairs. That is to say, it doesn’t matter if someone didn’t mean to deposit a certain sum in financial Alice’s account. If Alice’s routing and account number was used, the money will get deposited and therefore rightly credited to Alice. Likewise, if someone meant to vote for Bob but inadvertently checked Alice’s name on the ballot, then Alice will rightly get credited with a vote.

Such deposit and voting mistakes can and do occur. But the fact that they are mistakes, even unintentional ones, doesn’t change the true state of affairs. Yes, the mistakes might be corrected. Thus, the party that mistakenly deposited money into financial Alice’s account might request it back, and Alice’s bank may well return the funds. So too, the voter that mistakenly voted for Alice might be able to identify his or her ballot and redo it (this may be easier said than done given that ballots typically are secret ballots). But the point to appreciate is that in both contexts, an unintentional mistake in crediting money or votes will still be credited and recorded on the respective ledgers, and any corrections of the mistakes will likewise need to be recorded on the respective ledgers.

2. Some Differences Between Contexts

To the question “How did you vote?” a friend of mine used to quip “By secret ballot.” My friend’s quip underscores the fundamental difference between the financial and the electoral context. Money in a financial ledger always has an explicit provenance. There’s a source for the money and a tracking history of how it ended in, say, the ledger of financial Alice. This is not to say that Alice’s ledger is an open book for everyone to see. But those who need to know how money got moved in and off the ledger, from bank managers to tax authorities, will have the necessary access.

By contrast, ballots cast in an electoral context need to be received from registered voters, but then must be rendered anonymous so that no one can determine who cast which ballots (actually, as we’ll see later, this assumption allows an exception: voters themselves will be able to track their own ballots). Thus, when a ballot assigns a vote to either Alice or Bob, it must conceal the identity of the person who filled out the ballot as well as provide a record that this person actually did vote. This bifurcation of identifying the voter as having cast a legitimate ballot but then separating out the voter’s vote is necessary for free and fair elections. Without it, voter suppression and intimidation become much easier. But with it, electoral security becomes more difficult, though not impossible, as we’ll see.

It is instructive to see what an election looks like in which voter identity is linked to rather than separated from the votes cast. We see these types of votes in the U.S. Congress or Senate, in which members vote for or against some proposition and their votes are explicitly tied to their names (thereby allowing us to hold our elected representatives responsible for the votes they cast). Suppose similarly, in the election between Alice and Bob, voters did not need to conceal their identities in how they cast their votes. In that case, the ledgers for Alice and Bob would contain not just the votes they received but for each vote also the name of the person casting the vote. All voters would therefore be publicly identified with the votes they cast.

This suggests that in the electoral context with secret ballots, there’s still another ledger that needs to be kept track of besides the ledger recording votes for Alice and the ledger recording votes for Bob. That third ledger is the ledger of registered voters, and it must be continually updated to keep track of who has already voted and who hasn’t. Moreover, it’s also necessary to ensure that ballots of those who voted and were authorized to vote get properly credited to Alice or Bob.

But since those ballots are secret, it is not permissible to list them next to their corresponding voters on the ledger of registered voters. So where do the ballots end up? They can’t just be thrown away or deleted because then there’s no way to confirm that the votes voters cast were properly assigned. Even in the absence of bad actors committing election fraud, the possibility of mistakenly mapping the votes of voters to the wrong candidate (i.e., the candidate not voted for) requires safeguards, and that means keeping the ballots, whatever form they take.

Things are simpler on the finance side. With financial ledgers at banks (leaving aside physical currency, which is playing less and less of a role these days), deposits and disbursements are just authorized changes in numbers on the bank’s ledgers. It’s all digital these days, and it amounts to just adding a number to a row and column of a spreadsheet (or, more precisely, to a suitable location in a database), a positive number for a deposit, a negative number for a disbursement. It’s a bit more complicated in that the authorization of those changes needs to be tracked and confirmed. But it isn’t much more complicated than this.

Because the ballots are secret, however, elections require not just a third but also a fourth ledger, namely, a ledger of ballots. At first blush, it might seem that such a ledger would be unnecessary. After all, aren’t the different ways of filling out ballots extremely limited? Valid ballots will either mark Alice’s name but not Bob’s, or Bob’s name but not Alice. Invalid ballots would mark both Alice and Bob’s names or neither. It would seem that there are just four possible groupings of ballots, and that within each grouping, the ballots are indistinguishable.

But things are not so simple. The ballots come in at a particular places and times. That needs to be noted, if only to ensure that ballots filled out by registered voters at certain times and places are properly tracked and free of irregularities. Moreover, even though a ballot, by being secret, will lack information to identify the voter to anyone but the voter, yet it could contain further information, such as time- and place-stamps as well as possibly information recognizable only to the voter.

The secrecy of ballots would not be compromised with voters using in their ballots some markers of their identity, known only to themselves. After all, if you cast a ballot, it is your ballot. If the ballot is cast by someone else in your name, it is still your ballot, and you deserve to challenge it and get it changed. And if a mistake was made in who your ballot voted for (e.g., you know you voted for Alice but you see that the ballot that’s supposedly yours is sending your vote to Bob), you should likewise be in a position to challenge it and get it changed. Such markers could empower voters to make such challenges and changes.

Finally, besides such informational markers included by voters in their individual ballots, the ledger of ballots, much as the other ledgers, could employ digital technologies such as error correcting codes and other data integrity methods (including full-fledged blockchains). As we’ll see, data integrity of the ballots, especially with hidden markers that allow voters to verify their individual ballots, contribute effective safeguards against election fraud. Indeed, with a sufficiently robust ballot ledger, an entire election could be reconstructed.

As will become evident in this article, the ballot and registered voter ledgers are where the most important action lies in securing elections from mistakes and fraud. Unlike the financial context, an electoral context with secret ballots has four essential ledgers rather than two (additionally, the ledger of registered voters and the ledger of ballots). That’s a significant difference, and it has deep ramifications for election security, requiring security measures unlike those required for financial security.

One final note about these four electoral ledgers (i.e., Alice’s voting ledger, Bob’s voting ledger, the ledger of registered voters, and the ledger of ballots): unlike financial ledgers, which are behind a “need-to-know wall,” these four electoral ledgers are all intended to be open books. In other words, the public, which is voting for candidates Alice and Bob, should have access to all four of these ledgers, being able to track the precise changes to them in real time. This is not to say that there can’t be encrypted information in the ballot and registered voter ledgers, but information in these ledgers, whether encrypted or unencrypted, must be made explicit and fully available, even if it can’t be readily interpreted (for the moment) because of cryptographic safeguards.

TERMINOLOGY: The word “ledger” is, properly speaking, an accounting term. So my use of the word “ledger” both above and below is a bit loose. What I’m calling the ledger of registered voters and ledger of ballots would, in an accounting context, be called a “journal” of registered voters and of ballots. The distinction between ledgers and journals in accounting is this: journals are books of original or raw entry in which data is first entered, ledgers then distill and process that information from the journals. The ledgers of Alice and Bob, in the electoral context, would thus be closer to financial ledgers, extracting votes from the other ledgers (journals) and crediting them appropriately to Alice or Bob. At the end of the day, however, all these ledgers are databases with entries and groupings of entries timestamped and protected by data integrity methods.

3. Securing Against Financial Fraud

Let’s now turn to securing against financial fraud. We focus on financial Alice (the situation with financial Bob is parallel). Alice wants the record of deposits and disbursements in her ledger to reflect deposits that she has knowingly and willingly received as well as disbursements that she has authorized to go to the intended parties. If this is the case, the record of deposits and disbursements in her ledger as well as the running totals will correspond to the true state of affairs of what her transaction history and running totals ought to be.

In trying to secure Alice against financial fraud, we therefore need to consider what could go wrong. In fact, three things could go wrong:

1. Alice finds a disbursement that she did not authorize.
2. Alice finds a disbursement that she did authorize but that went to an unintended party.
3. Alice fails to receive a deposit that she was supposed to receive.

All three cases represent a failure. With fraud, we consider them a failure of security. With unintended error, we consider them a failure of numerical input, calculation, or technology.

But given that unintended errors could always be intentional (though the intentionality may be implausible, as with certain types of common math errors), and given that the damage done by unintentional errors can be as profound, and sometimes more so, than done by fraud, it is convenient to treat all such failures, at least potentially, as cases of fraud and to strive to protect against them. (For an unintentional math error that, in 2012, caused J.P. Morgan Chase to lose $6B dollars, see chapter 3 of Matt Parker’s Humble Pi.)

We therefore consider a bad actor, the fraudster Frank. Frank is going to try to divert money from Alice’s account so that disbursements intended for Bob end up on Frank’s financial ledger, or deposits intended to go on Alice’s ledger likewise end up on Frank’s financial ledger. How could this happen?

Let’s ignore microthefts, in which pennies or even fractional pennies are skimmed off an account at every transaction, making the thefts numerous but almost unnoticeable. Instead, let’s focus on large discrete events where the fraud is palpable. Thus, it could happen that Alice authorizes a disbursement intended for Bob, but it never ends up in Bob’s account. Or Alice might be informed that a deposit into her account is on its way, say from Bob, but it never arrives. Or it might happen that funds simply disappear from Alice’s account without her authorization.

To commit fraud in such cases, what might Frank do and what safeguards might hinder him from committing the fraud in the first place? As noted earlier, money transferred among bank accounts (such as the financial ledgers of Alice and Bob) always has a provenance. Money can’t just magically materialize. There’s always a history. For money to be deposited in one account, it must be withdrawn from another account, and there has to be a record of the transaction. The only exception is the fiat creation of money by the central banks, in which they create a deposit without transferring existing funds. But even here there has to be a record of the money being created.

Let’s therefore start with fraudulent disbursements. Prior to a given transaction, Alice is, let us say, satisfied that all earlier transactions are legitimate. We can assume that data integrity methods are in play so that Alice and impartial third parties can all agree that up to the problematic transaction, all the prior transactions are legitimate. So let’s say $10,000 was transferred out of Alice’s account without her authorization. How could this have happened? Let’s run through the possibilities.

3.1 Magical Dematerialization

The money just disappeared. In this case there would be no record of any authorization by Alice, or by someone impersonating Alice, or by any bank official that she disbursed the funds. This would represent a cybersecurity failure on the part of the bank, and the bank would clearly be liable. Perhaps outsiders were able to hack into the bank’s computers. Perhaps insiders were able to subvert the bank’s cybersecurity.

Cybersecurity measures exist to prevent such fraud. With such an eventuality, the first question is, Where did the $10,000 go? Unless, per impossibile, the money simply vanished without a trace, whatever entity owns the account to which the money was first transferred would immediately be suspect, though in a money laundering scheme, the money would be quickly transferred elsewhere, perhaps multiple times, to break the trail and keep the fraudster Frank in the shadows.

Of course, given Frank’s ability simply to make money dematerialize, (i.e., to transfer it without any authorization), it seems that Frank should not simply have stopped with $10,000. Instead, he should have cleaned out Alice’s account entirely, and that of the other account holders, and then perhaps also corrupted or even crashed the bank’s computers.

With data integrity methods in place, however, it would still be clear when the fraud happened and what damage was done. The worst blame in all this would fall on the bank for not securing its technology against bad actors like Frank, who can be expected to be bad. The bank, however, is not expected to be digitally incompetent. <<<<

3.2 Faking Authorization by Alice

The money left Alice’s account, and there’s a record of Alice authorizing the transfer, but in fact Alice did not authorize it. This sort of fraud happens regularly with debit cards that are used at ATM machines or at stores to make purchases. The debit cards are stolen or cloned, and the bad actor Frank uses it, with Alice’s seeming authorization, until the fraud is discovered, after which he discards the card and likely attempts to repeat the fraud under another guise, unless or until he is caught.

With debit cards there’s a limit to how much the account can be debited. Common daily caps are $200 for ATM machines and $2,000 (plus or minus) for purchases. Thus there is a limit to how much damage Frank can do to Alice in such cases, the fraud usually being quickly detectable. In fact, because of FDIC insurance, Alice should be able to recover her loss by notifying the bank and issuing an affidavit that there was fraud on her debit card. A new debit card will be issued, and Alice’s account will be credited with the money that was stolen.

A debit card used to withdraw funds from Alice’s account serves as a proxy for Alice. It’s as though Alice is authorizing the withdrawal of those funds by means of the card. Someone who steals or clones the card is therefore essentially impersonating Alice, using the card to authorize, in Alice’s name, the withdrawal of funds.

However, for larger withdrawals, such as $10,000, a debit card won’t work. Any faked authorization for such a disbursement will require gaining hold of Alice’s identity to a greater of lesser extent. It could be as simple as getting into Alice’s online checking account via her username and password. It could also require getting hold of Alice’s “challenge questions,” posed during the login process to ensure that it really is Alice (e.g., “Where did you meet your significant other?”). And a two-step verification using Alice’s cell phone could add further safeguards to ensure Alice’s identity.

None of these security measures is foolproof. As a consequence, banks need to allow that such fraud can happen, much as they allow for and anticipate cloned debit cards, but also build in some damage control. An obvious place for such security measures is to limit what can be disbursed via online checking. If $10,000 is over the limit, then hacking into Alice’s online checking account won’t be able to transfer that amount. Indeed, Alice herself may want to place limits on the total amount of any single disbursement from online checking as well as any total over a given time frame.

Banks and credit card companies have also gotten good, via machine learning, of discerning patterns in the financial transactions of their users and flagging inconsistencies. This is not an exact science, yielding up false positives as well as false negatives. But it’s better than nothing. By setting a low threshold for false positives, and thus flagging a lot of seemingly suspicious transactions actually authorized by Alice, the banks minimize false negatives but also increase the inconvenience to Alice by more frequently having to query her, “Did you authorize this expenditure? Reply YES or NO.”

Frank still has two tricks up his sleeve to defraud Alice: paper checks seemingly signed by Alice and wire transfers in Alice’s name. Paper checks with Alice’s supposed signature will require stealing checks from Alice or counterfeiting them and then forging her signature. There is a danger here that fraudulent checks so used will cause money to disappear from Alice’s account, but precisely because there’s a real paper trail (and not a purely digital trail), the process of transferring the funds tends to be slow and the danger is mitigated. In attempting to deposit such a fraudulent check, Frank will likely face a bank that wants to hold it for a given time before releasing the funds and also to confirm with the issuing bank that it is legitimate. Thus Alice’s bank may even contact her to confirm the check’s legitimacy.

A wire transfer (and a cashier’s check), by contrast, remove funds immediately from Alice’s account and thus will require Alice, or someone the bank mistakes for Alice, to show up at the bank and authorize the wire transfer (or cashier’s check). That’s requiring quite a bit from the fraudster, though that’s not to say it can’t be done. But Frank, or an accomplice, will need to impersonate Alice and be able to jump through quite a few hoops in order to abscond with her funds. The degree to which the bank knows its customers will limit Frank’s ability to carry out this fraud. <<<<

We’ve now considered the main lines of attack by which Frank might defraud Alice, and where there’s a burden on Alice to protect her account (or ledger). Leaving aside cybersecurity safeguards put in place by Alice’s bank, which may be solid or less so, Alice’s main task is to protect her identity and keep Frank from co-opting aspects of her identity that would allow him to authorize disbursements from Alice’s account. Moreover, by putting caps on the amounts that may be disbursed from her account, even with varying levels of authorization, Alice supplies her account with further safeguards.

Other fraud is possible with Alice’s account, but the burden in these cases falls not on Alice. If Alice authorizes a disbursement to Bob and the amount is withdrawn from her account, but Bob never receives it because Frank has diverted it, Alice will have good evidence that she authorized the disbursement and intended to send it to Bob (by, say, verifying that she used the correct routing and account number to Bob’s bank). Alice has acted in good faith. The fact that Bob never received the money is on Alice’s bank, or Bob’s bank, or on intermediary channels through which the money needed to go but from which Frank managed to divert it. The possible cybersecurity failures here are immense and will need to be handled on a case-by-case basis.

Finally, there’s the inverse of the previous fraud, in which Bob authorizes a disbursement to Alice, has solid confirmation that he did indeed authorize it, sees his account debited accordingly, but Alice never receives the funds and can verify as much. Neither Alice nor Bob has done anything wrong, and the breakdown in cybersecurity must again be ascribed to the respective banks of Alice and Bob and any intermediate channels connecting the two. In either case, Alice authorizing a transfer of funds that leaves her account but never makes it to Bob, or vice versa, Alice and Bob have done everything in their power to protect themselves.

A postscript is now worth adding. I mentioned the FDIC, or the Federal Deposit Insurance Corporation, which provides insurance on people’s bank accounts, up to $250,000 for each account. If there is provable fraud on a bank account, with funds absent that should be there, banks are thus not only obliged but also ready to make up the difference because they can offload the cost to the FDIC. The point to note is that in the electoral context there is nothing like an FDIC. If there is fraud, the voter is left holding the bag.

If the voter’s ballot was lost or altered or if bogus ballots were mixed in with legitimate ballots, voters have no recourse to a third party like the FDIC to “make things right.” It’s up to the voter to prevent the fraud from happening in the first place. That’s why advice by the Roman orator Quintillian, suitably adapted, needs to apply to elections. In advising aspiring writers, Quintillian urged: “Write not so that you will be understood but write so that you cannot be misunderstood.” The lesson to voters is this: Don’t submit ballots in the hopes that they will be properly counted but submit ballots so bulletproof that they cannot be miscounted.

4. Securing Against Election Fraud

The role of the voter in the electoral context has no parallel in the financial context. As a result, a significant difference exists in the roles of financial Alice and Bob versus electoral Alice and Bob. In the financial context, Alice, Bob and others like them (Carol, David, Earnest, etc.) are financial agents that consciously move money, or capital, among themselves. In the electoral context, all capital consists of votes and arises from voters casting their ballots for Alice or Bob. Unlike financial Alice and Bob, who move money around, it’s not for electoral Alice or Bob to move votes around. Rather, their overriding concern should be to make sure that votes for either of them get properly counted.

So, in trying to secure Alice against electoral fraud (and likewise Bob), let’s start by asking what should go right as voters cast their votes. Ideally, all voters should be properly entitled to vote, no voter should vote more than once, all ballots should represent votes by legitimate voters, all ballots should be unambiguous in who they voted for, all tallies (intermediate and final) of votes for candidates should be accurately computed and accurately assigned, and the real-time tallies for any candidate should be, as mathematicians say, “monotonically increasing,” in other words, they should, like a ratchet, keep going up and up. If a vote tally at any point goes down, subtracting votes from a candidate, that will need to be duly noted and will represent a mistake that needs to be fully accounted for.

Given this list of desired features for a fair election, let’s now turn the question around and ask what could go wrong to prevent a fair election. In answering this question, let’s be clear about the different actors in play. There are Alice and Bob, who by the time that ballots are cast will be largely finished with campaigning and should have little more to do than sit back and await the outcome. There are the voters, who now need to decide the election with their ballots. There’s the election commission, which is supposed to make sure that the will of the voters is accurately represented by duly securing the ballots cast and correctly assigning vote tallies to Alice and Bob. There are the poll watchers and other independent parties interested in monitoring the election and ensuring a fair outcome. And then there are the bad actors, who need not be mutually exclusive from any of the above, though they may also include additional players (e.g., foreign governments).

What are the different types of bad actors who commit election fraud? Bad actors can include individuals who are not entitled to vote but who nonetheless cast ballots that get counted for Alice or Bob. They include voters who are entitled to vote, but who vote more than once for Alice or Bob (perhaps by being registered to vote in more than one state and by voting in different states if the election between Alice and Bob is a national election). They include more ambitious criminal enterprises that somehow manufacture votes en masse and get them credited to their preferred candidate. And they include an election commission that is lax, whether on purpose or by incompetence, or simply corrupt, whether enabling other bad actors to fraudulently influence the election results, or even actively engaging in the fraud itself. A fraudulent election commission is a classic case of Quis custodiet custodes? or Who’s minding the minders?

Given these different ways that election fraud can arise, what security precautions should be in place to prevent or at least limit it? Here are some recommendations. They provide a springboard to the Cryptosecure Election Protocol outlined in the next section.

1. Maintaining a clean ledger of registered voters. There needs to be perfect clarity about who may legitimately vote and who may not. The ledger of registered voters needs to be fully specified and publicly available. It must be regularly purged of people who have died or otherwise lost their qualification to vote. The ledger must also purge any duplicated references to the same person. Finally, it needs to disambiguate different individuals with the same name.
2. Qualifying to get on the ledger of registered voters. Only people legitimately entitled to vote should be able to register to vote and thus get their names to appear on the ledger of registered voters. There’s a need for balance here so that the requirements to register are not so arduous as to discourage voters (voter suppression) but also not so lax as to allow unqualified people to register.
3. Noting who voted. When someone casts a vote for Alice or Bob, that fact should be immediately noted next to that person’s name on the ledger of registered voters. It needs to be clear who voted and who didn’t.
4. Verifying who voted. At the same time that someone casts a vote for Alice or Bob and that vote is noted on the ledger of registered voters, it also needs to be verified that the person who voted is indeed the person on the ledger whose name is being checked off as having voted. The verification procedure for verifying that the person voting corresponds to the person said to be voting needs to be highly reliable but also not so arduous as to discourage voters. Nevertheless, if someone shows up to vote, claims it is for the first time, but is refused the opportunity to vote because the ledger of registered voters shows that the person did already vote, there has to be a way for this voter to challenge the existing vote that was cast in his or her name. If the challenge fails, it needs to be because the voter making the challenge already voted or is not in fact the voter that he or she claims to be. If, on the other hand, the challenge is legitimate because the actual voter was impersonated, it should be possible to invalidate the earlier fraudulent vote and validate the vote by the actual voter.
5. Preserving the record of ballots. When someone votes and the vote is noted on the ledger of registered voters, what happens to the ballot casting the vote? Ultimately, the ballot belongs to the voter. So data integrity methods should prevent the ballot from being changed or tampered with once it leaves the hands of the voter and is delivered to the election commission for counting. In particular, all those ballots should be preserved. It should be clear if any ballots have been lost, and, if so, how many. The ballots should include date and time stamps, as well as crypto-secured identifying information from voters, who with this information should be able privately to identify whether their ballot was indeed lost or tampered with. Moreover, it should be clear for any ballot which vote it corresponds to on Alice’s or Bob’s ledger of vote tallies. Finally, for any vote recorded on Alice’s or Bob’s ledger, it needs to be clear whether it corresponds to a preserved ballot or a lost ballot. The desired items described under this bullet point may seem unrealistic, but they are in fact workable.
6. Enforcing transparency of the electoral process. Poll watchers and independent parties, whoever they are and without restriction, should be able to scrutinize any aspect of the electoral process, subject to the one condition that voters must be able to vote for Alice or Bob without divulging their identity. Everything else in the electoral process should be open to scrutiny. It must be possible to track vote totals on Alice’s and Bob’s ledger in real time, and there must be a clear chain of justification any time votes are added to, removed from, or transferred among these ledgers. The ledger of registered voters, especially as “check marks” are put next to names of people said to have voted, must also be open to inspection in real time. And most importantly, the ledger of ballots needs to be open to scrutiny, with any tampering of or losses to ballots being instantly chronicled.

With all six of these bullet-point recommendations for ensuring a fair election between Alice and Bob, data integrity methods need to be used throughout. Elections happen in time and over time, so there is always a history. All four of the election ledgers (of Alice, of Bob, of registered voters, and of ballots) are built over time. Every addition, subtraction, and edit to these ledgers happens in real time and needs to be noted. Data integrity methods make sure that anything recorded on any of these ledgers at one point in time is faithfully preserved at a later time.

5. A Cryptosecure Election Protocol (CEP)

We now come to the most interesting part of this article, namely, a cryptographically based protocol for securing elections. If such a protocol can be made to fly, it will do much to secure free and fair elections as well as to boost voter confidence that votes are being accurately counted and not mixed with fraudulent votes. I want in this section to argue that the tools of cryptography actually do allow for such a protocol. I will lay it out briefly, yet in sufficient detail, to (hopefully) convince readers of its feasibility.

5.1 The Unnecessity of Dedicated Voting Machines

First off, the Cryptosecure Election Protocol (or CEP) will be formulated independently of any dedicated voting machine. It is really quite remarkable, and even ridiculous, that elections should use and depend on dedicated hardware devices that run proprietary black-box algorithms (protected by patents no less). It’s like creating a market for horse and buggy when Tesla electric vehicles exist.

To understand why dedicated voting machines should be a thing of the past, consider that we live in an age of smartphones, which by the standards of 25 years ago (given Moore’s Law) are supercomputers. These smartphones are all-purpose computers. We no longer need to buy a separate metronome, a separate mp3 player, a separate video recorder, a separate stopwatch, etc. With the right apps, smartphones are all-in-one computational devices. So are current laptop and desktop computers.

Smartphones illustrate what may be called “the Turing Principle,” after the key figure in modern computing, Alan Turing. Usually, in computer science, this principle is called the Turing Thesis (or the Church-Turing Thesis, giving additional credit to the logician Alonzo Church, Turing’s dissertation supervisor). The Turing Thesis states that all computation can be done with a few very simple algorithmic building blocks, such as addition, subtraction, instructions for changing memory locations, and conditional transfers of control (i.e., if this, do that, otherwise do something else).

The Turing Principle is less formal than the Turing Thesis. It’s point is that all working computers are essentially the same and that in practice the only difference is speed and memory. So, with regard to elections, the point of the Turing Principle is that there’s no need for uniquely purposed hardware or software to keep track of votes. The Turing Principle instantly dispenses with voting systems that employ both physical machines running proprietary software, such as the Dominion Voting Systems. But, it also dispenses with virtual machines running proprietary software that centralizes all voting activity under under a single corporate authority, such as Voatz.

5.2 Structure vs. Function

What’s needed for a credible voting system is that any hardware and software used in voting perform certain verifiable functions, regardless of the underlying hardware and software used. It’s the classic distinction between structure and function. Voting machine companies provide structures — hardwired or virtual machines running particular proprietary algorithms. Instead, free and fair elections require verifiable functions — things that machines, regardless of underlying structure, can do, and in ways that we can verify.

So let’s get started with the CEP. Given the 2020 U.S. presidential election, in which ballots took many different forms, and where show-up-in-person voting played a diminished role because of widespread mail-in ballots, the CEP will be formulated for purely digital ballots. This, it seems, is in fact the future of voting. Interestingly, it also allows for more secure elections than going non-digital.

Those who witnessed the transition from typewriters to word processors in the 1980s will remember the resistance to digital documents, which were at the time treated as less securely preserved than paper documents. But in the end, we’ve come to regard the digital as more secure, capable of being housed in multiple virtual locations, being immune to fire, loss, and degradation, and being readily searchable.

Digital ballots promise a similar advantage over paper ballots. The CEP can accommodate a hybrid approach that also uses paper ballots, but only by digitizing the paper ballots and thereafter treating them the same as ballots that were digital from the start. Despite this possible flexibility, we’ll be purists here and develop the CEP for purely digital ballots.

5.3 Alice’s and Bob’s Ledger of Votes

The election is between Alice and Bob (for simplicity, let’s assume no other candidates and no other offices up for election — generalizing to more candidates and offices is straightforward). So there is Alice’s ledger of votes in her favor and Bob’s ledger of votes in his favor. The election commission can set up a website for the election, let us say at alice-v-bob-election.gov. Alice’s ledger of votes can then be recorded at alice-v-bob-election.gov/alice and Bob’s at alice-v-bob-election.gov/bob.

These two ledgers can be updated in real time. Poll monitoring organizations, especially those sponsored by the political parties to which Alice and Bob belong, will monitor these sites and use data integrity methods (notably hashing and blockchains) to ensure that any changes at any given point in the election are made to ledgers whose integrity has been confirmed up to that point. Ensuring data integrity in this way is well-worn ground, and here’s no need to rehearse it here.

On a side note, even without formal cryptographically based data integrity methods, Internet users have invented the virtual equivalent through caching and screenshots of web content. For instance, if someone posts something on Twitter and then removes it, or if someone posts something on a blog and then revises it to remove an embarrassing detail, because Internet users are constantly caching and taking screen shots of online content, it’s virtually impossible to remove or deny anything that has appeared online. Data integrity methods simply make the process of verifying and preserving digital content more formal and foolproof.

5.4 The Ledger of Registered Voters

The ledger of registered voters needs to be considered next and can reside at alice-v-bob-election.gov/registered-voters. This ledger gets updated in real time, so, as with alice-v-bob-election.gov/alice and alice-v-bob-election.gov/bob, the ledgers of Alice and Bob, the ledger of registered voters will likewise be monitored and preserved using data integrity methods.

In building the ledger of registered voters, we start with a ledger of eligible voters, say, at alice-v-bob-election.gov/eligible-voters. Though it (and the other ledgers) will actually be a relational database, we can imagine it as a giant online spreadsheet with first name, middle name, last name, and alternate names in different columns, each row corresponding to a single eligible voter. Other voter information (address, age, etc.) may need to be present to disambiguate names (how many eligible voters have the name “John Paul Smith”?).

5.4.1 Proof of Identity

To be a registered voter, and thus have one’s name moved from the ledger of eligible voters at alice-v-bob-election.gov/eligible-voters to the ledger of registered voters at alice-v-bob-election.gov/registered-voters is going to require proof of identity (PoI). Thus, it’s going to be up to the election commission to gather such PoI information and up to each voter to supply it. There has to be a collaboration here. To be a registered voter is more than simply being an eligible voter and requires some act or effort that clearly identifies and thereby authorizes a voter to vote in the election between Alice and Bob.

Security and privacy concerns now become important and will need to balance each other. Imagine, for instance, a voter comes into the election commission offices and identifies him- or herself as a particular voter. The election commission can attempt to confirm the voter’s identity by asking for a state-approved photo ID. But it could go much further. It could ask for biometric authentication and identification, everything from fingerprints to retinal scans to gait analysis. Asking for a state-approved photo ID seems pretty minimal. Asking for full-fledged biometric data seems a bit much.

The entire procedure for gathering PoI data and thus registering a voter could conceivably be put online. For instance, in some states it’s possible to apply for one’s birth certificate online by answering certain challenge questions about one’s life and activities (state and federal government seems to track our movements quite precisely and know the “right questions” to ask). This information plus a payment by bank draft or credit card can be enough to secure a valid birth certificate.

Whatever the information used to establish PoI and however it is gathered, it will need to captured digitally. Thus, if a photo ID is used, a digital scan of it will need to be preserved. If biometric data are used, they will need to be preserved, perhaps via digital video. Likewise with any other information used to establish PoI. So, for a given name N taken from the ledger of eligible voters, there will be a data file Z (it can be a lossless compression ZIP file) that contains all such evidence establishing proof of identity (PoI).

The data Z allows for the name N to be moved from the ledger of eligible voters to the ledger of registered voters. Yet because the list of registered voters is publicly visible at alice-v-bob-election.gov/registered-voters, confidentiality requires that the information in Z be hidden from the public. To that end, the election commission will put next to the name N not the PoI data Z itself, but a hash of it, i.e., hash(Z). Because Z is N’s data as much as, and indeed more so than, the election commission’s, both N and the election commission will have full access to Z. Both will keep it confidential, yet both can make it available as needed.

Hash functions are widely known and used, especially in cybersecurity. They are one-way functions, which is to say they are easy to compute but hard to invert. Hash(Z) can therefore be quickly calculated, yet it is virtually impossible (i.e., with extremely low probability) to reverse it and find what data returned a given hash value simply from that value. (In fact, hash functions tend to compress information, even reducing megabytes to a few hundred bits, so technically speaking the challenge is not to invert them but to find a preimage that maps onto a given hash value.)

So, if someone sees hash(Z) but doesn’t know that it came from Z, there’s no way for this person to determine Z. And yet, if someone tries to tamper with Z and say that instead the PoI information for N was not Z but instead W, it will be instantly clear that this can’t be because hash(W) will with overwhelming probability not equal hash(Z). Data that is very similar, that differs even in only one place, will yield extremely different hash values. Hash functions are extremely discontinuous, so data that look very similar (perhaps differing in only a single bit) will yield completely different hash values.

A common hash function is the Secure Hash Algorithm created by the National Security Agency and distributed by the National Institute of Standards and Technology. It happens also to be the hash function used by Bitcoin. SHA-256 maps arbitrary strings to strings of 256 bits, or 64 characters in hexadecimal notation. It’s easy to find SHA-256 calculators online (here’s one).

5.4.2 The Worry of Technology Overload

I want to step back for a moment and consider the worry of “technology overload” on the average voter N. For instance, am I, in proposing the CEP (Cryptosecure Election Protocol) really expecting voters to find an SHA-256 calculator and use it to compute the hash of their PoI data Z? Yes and no. No in the sense that voters will not need to know any of the nuts and bolts of these technologies, but Yes in the sense that via convenient apps (actually, a single app could handle the entire CEP), voters will nonetheless be performing the underlying functions. Apps can readily compute SHA-256, and the hash values computed can be readily stored as QR codes or other matrix barcodes.

Because the CEP depends entirely on the performance of verifiable functions, any apps that voters use will be interchangeable with other apps that perform the same function. If a voter belongs to a particular political party, it will be likely that the party will supply such apps to its members. To avoid false flag recruitments, however, it may be advisable to go with independent third parties, especially those that guarantee privacy and the absence of user tracking.

5.5 Two Public-Private Cryptographic Key Pairs (Four Keys Total)

To round out the protocol, the voter N will now need to generate two public-private key combinations (E,D) and (E’,D’) with respect to a reliable public-key cryptosystem. E and E’ represent the encryption keys of a public-key cryptosystem, D and D’ respectively the decryption keys. In public key cryptography, the public is given an encryption key, so that it can encrypt messages at will, but decryption requires also knowing the decryption key, which is kept private to the user generating the key combination.

As the Wikipedia article on public-key cryptography explains in the caption to the following diagram, in an asymmetric or public-key “encryption scheme, anyone can encrypt messages using the public key, but only the holder of the paired private key can decrypt. Security depends on the secrecy of the private key.”

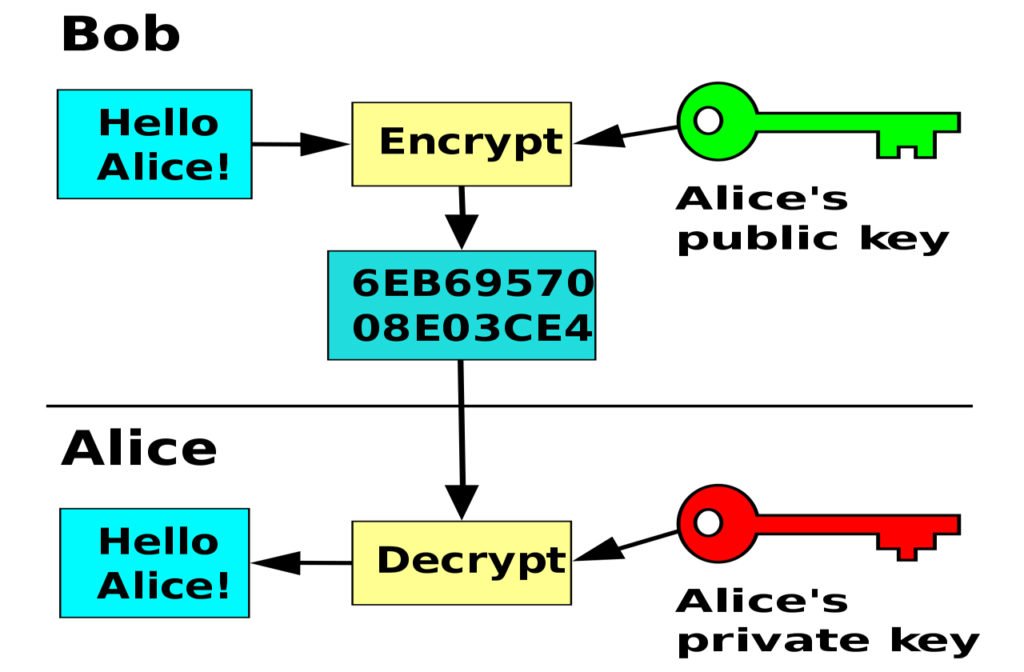
For our purposes in the CEP, RSA (Rivest-Shamir-Adleman) public key cryptography would be fine, but so would DSA (Digital Signature Algorithm) or ECDSA (Elliptic Curve Digital Signature Algorithm).

Why is a voter N going to need two public-private key combinations (E,D) and (E’,D’)? The reason is that voters, in order to vote in secret, need to separate their identity from their ballots in dealing with the public and with the election commission. This means there needs to be a way for voters to ensure that their ballots are duly recorded (hence one public-private key pair) and that they can identify their ballots even if others can’t (hence the need for another pair). Moreover, voters will need to be able to prove to others that their votes did or did not get adequately counted. Public-key cryptography, used with two key pairs protects voter confidentiality and assures voters that their votes are properly counted. Again, it’s all about the voter.

For convenience, let’s now imagine that the voter N has email address [email protected] and cell number 555-555-5555. This information can be included in the PoI data that N provides to the election commission. In addition, the PoI data needs to include E (from the public-private key combo (E,D)) and a hash of D’, i.e., hash(D’) (from the public-private key combo (E’,D’)). By hashing the private key D’, N effectively hides D’ from others but can reveal knowledge of D’ to others by, if needs be, revealing D’ and showing that it does indeed equal the value previously assigned to hash(D’). All this information is then incorporated into the PoI data file Z.

The election commission then securely emails Z as an attachment to [email protected] (perhaps with two-step verification using N’s cell number before hitting “send”). Next to N’s name at alice-v-bob-election.gov/registered-voters, the election commission now puts hash(Z). And N, with an app that computes the hash function, confirms that the attachment sent to [email protected] has a hash that indeed computes to hash(Z) as on the server.

Such confirmations can be quickly accomplished with QR barcodes (the “QR,” after all, refers to “quick response”). If at any point what’s appearing on the election commission’s server does not agree with what N thinks should be there, N, or a third-party representative, can challenge the election commission and prove (this is the crucial point) that the election commission’s data has been compromised. Yet because compromises to data integrity can be so easily uncovered, we can expect the election commission to be incentivized to keep such incongruities to a minimum.

5.6 Securing Against Loss of PoI Data

So far the data recorded next to N’s name at alice-v-bob-election.gov/registered-voters looks like <N, hash(Z)>. This voter array needs to be expanded. It needs to be clear that the election commission is preserving, as in backing up, the PoI data that makes up Z. The problem is that hash(Z) comprises only a few bits of information (256 with SHA-256), so for big zip files Z, it will be impossible to reconstruct Z simply from the hash value hash(Z), and that would be true even if the the hash function were readily invertible (which it is not).

Granted, N is supposed to keep a copy of Z. But if there is identity fraud in which the election commission itself or other bad actors are attempting to create voters out of thin air, it’s going to be important for independent parties to be able to examine the actual PoI data for each supposed voter. The election commission therefore needs to preserve Z and not be able to claim that Z was lost. To that end, N’s voter array should also include encrypt(Z), namely, a lossless encryption of Z by the election commission, which it makes public, which it can decrypt at will or be ordered to decrypt by a court, and which will prevent it from losing or claiming to have lost Z.

5.7 Rounding Out the Voter Array

In addition to encrypt(Z), the voter array for N also needs to include E, the public key of the public-private key pair (E,D), and hash(D’), a hash of the private key of the public-private key pair (E’,D’). So the entire voter array for N at alice-v-bob-election.gov/registered-voters will look like <N, hash(Z), encrypt(Z), E, hash(D’)>. Because Z will always be unique for a given voter N and because large-scale randomization is used to choose public and private cryptographic keys (especially because these keys are generated by enlisting combinatorial explosion), all entries in these voter arrays will (with overwhelming probability) be unique, with no overlap from one voter to the next.

A voter array, as a 5-tuple, may seem a bit complicated, but it is necessary. It is also easily managed through online databases and user apps. The dominant theme in the Cryptosecure Election Protocol is the primacy of the voter. All the data associated with a given voter in an election belongs to that voter, and it must be possible for the voter to confirm the accuracy of the data. The PoI data for N, therefore, does not belong, in the first instance, to the election commission. The election commission is the trustee of the data. But because not all trustees are trustworthy, the voter needs at every point to be able to verify that the election commission is doing its job. The CEP is all about the voter, eliminating the need for trust and empowering the ability to verify.

Before moving to the ledger of ballots and how votes are actually assigned, I need to address a concern just touched on, namely, creating registered voters and their voter arrays out of thin air. For actual voters N who are able to get their voter arrays <N, hash(Z), encrypt(Z), E, hash(D’)> reliably positioned at alice-v-bob-election.gov/registered-voters, their votes will, as we shall see, be secure. The worry, however, is that bad actors will simply create new voters from thin air or else set up voter arrays for eligible voters who are either not planning to vote at all or planning to get registered and to vote at a later date but then find themselves already registered under a proof of identity that they did not authorize.

For voters who find themselves already registered under another PoI with public and private keys not of their choosing, they will need, and presumably have, substantial recourse to challenge the election commission (as in other cases of identity fraud involving trusted third parties). More worrisome are the voters created out of thin air (or exhumed from the grave) and those who never vote but have their identities co-opted and then are made to vote, presumably for the candidate chosen by the bad actors guilty of creating these novel voter identities.

Fortunately, because the proof-of-identity data Z is cited in the voter arrays and can be reconstructed on demand (perhaps by a court order), it will be possible to scrutinize such data and find irregularities that call into question any ballots fraudulently created by forging identities. Challenging bogus listings in the ledger of registered voters becomes evidentially stronger if the actual voters supposedly responsible for them can be located and these voters can confirm that the listings are indeed bogus. Otherwise, the evidence that there was fraud will be more circumstantial.

5.8 The Ledger of Ballots

Let’s now turn to the ledger of ballots. The ledger of ballots can be housed on the election server here: alice-v-bob-election.gov/ballots. For N to cast a ballot will require two steps or, technically, two uploads. These uploads can occur at

• alice-v-bob-election.gov/ballots/ballot-upload and
• alice-v-bob-election.gov/ballots/key-upload

We can imagine the ballot to be a pdf fillable form with a box next to Alice’s name and one next to Bob’s name. N will check one and only one of the boxes (in fact, as a fillable form, the possibility of checking two boxes should be precluded). In addition, N will add what’s called a cryptographic nonce to the form, some field that will hold a substantial novel random number, perhaps 50 to 100 digits, or more. The nonce helps ensure that ballots, all of which will be encrypted, don’t all encrypt just two digital ballot files (one with Alice’s name checked, one with Bob’s name checked), thus safeguarding against preimage attacks that depend on knowing details about the data that was encrypted.

5.8.1 Uploading an Encrypted (or Reverse-Encrypted) Ballot

Given a ballot V (N’s voting ballot), N now encrypts it using not the encryption key E’ but its corresponding decryption key D’, i.e., D'(V). Applying decryption in this way is a common way of cryptographically signing a digital file, such as V, and shows to anyone who applies E’ to D'(V) (= E'(D'(V)) = V), thereby recovering V, that the person who knows D’ did indeed form D'(V). Note that first decrypting and then encrypting cryptographically parallels first encrypting and then decrypting and returns intact the thing we started with.

N now performs two uploads. At alice-v-bob-election.gov/ballots/ballot-upload, N uploads D'(V). To authorize the upload, N is presented with a challenge question, namely, to decrypt some text T that was encrypted with the public key E (not E’) to form E(T). By decrypting E(T) using D, N proves to the election commission (or its servers) that it really is N on the line. This approach would require varying T, presumably randomly, from voter to voter.

An alternative approach would be to fix T and have the N compute D(T) so that when the E is applied to it, T is returned (i.e., E(D(T)) = T). Either approach can be made to work, confirming that N is on the line and thereby authorizing N to upload D'(V). The role of the public-private key (E,D) is therefore purely to confirm N’s identity and thus to authorize N to upload a ballot and thereby vote.

Once D'(V) is uploaded, it immediately appears at alice-v-bob-election.gov/ballots, and N’s voter array at alice-v-bob-election.gov/registered-voters is marked as having voted, i.e., <N, hash(Z), encrypt(Z), E, hash(D’), voted>. N will be able to confirm that D'(V) was indeed just uploaded, perhaps by using QR barcodes.

The election commission, if unscrupulous, could attach some sort of tracking pixel to D'(V) to connect this ballot with the voter N (who had to use E, and thereby divulge his or her identity, to upload D'(V)). But any such pixel will be extraneous to D'(V) and, because elections are supposed to be conducted by secret ballot, would be strongly proscribed, even by law. D'(V), because it is encrypted (or, if you will, reverse encrypted, or “cryptographically signed” by N) will by itself offer no insight into who received a vote from this ballot, whether Alice or Bob. D'(V) will therefore, immediately after its upload, reside as a yet-to-be-counted ballot at alice-v-bob-election.gov/ballots, awaiting further instructions from N before it can actually be counted.

5.8.2 Uploading the Public Key

For the encrypted ballot D'(V) to be counted, N therefore needs to do one more thing, namely upload the public key E’ (not E) at alice-v-bob-election.gov/ballots/key-upload. N will do this anonymously. All N needs to do is get E’ loaded and visible at this location on the server. Again, QR barcodes can simplify confirming that E’ has been indeed uploaded.

The election commission will want to avoid spamming and denial of service attacks, so uploading public keys at alice-v-bob-election.gov/ballots/key-upload will require some mechanisms to slow down the number of uploads, such as safeguards against robots and marking some boxes guaranteeing that the person uploading the key is qualified to vote in the election between Alice and Bob.

In fact, it doesn’t much matter how many extraneous keys are uploaded so long as it’s not too much as to overwhelm the server. Voters might even be given special access codes, not specific to particular voters, but still enough to block the efforts of bad actors to interfere in the election by uploading too many extraneous keys that would serve no role in the actual ballot counting except as spam or denial of service.

5.9 Trying All the Keys on All the Locks

So what happens when not only N but all voters like N, in two separate uploads each, upload their reverse-encrypted ballot D'(V) and the public key E’. Each voter N will be able to confirm that both D'(V) and E’ are listed on the ballot server alice-v-bob-election.gov/ballots. Essentially what we have then is a two-dimensional array of reverse-encrypted (but therefore still encrypted) ballots down one side of the array and all the public keys (perhaps with extraneous ones) down the other.

Here’s a crude diagram to illustrate the point. We imagine seven voters, “a” through “g,” that cast ballots Va through Vg by signing or reverse encrypting them with private keys D’a through D’g. And we further imagine seven public keys E’1 through E’7. The boxes in the two-dimensional array or grid then represent possible combinations of cryptographically signed ballots and public keys, and the asterisks represent where a public key E’ unlocks a ballot D'(V):

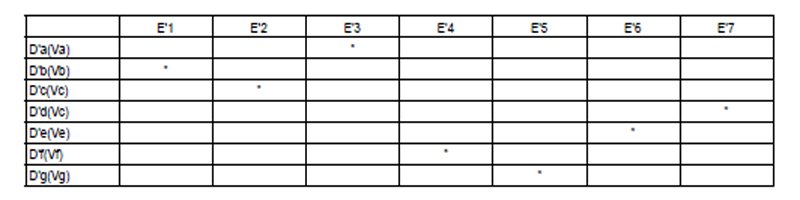
Each public key will unlock at most one reverse-encrypted ballot. If N is a legitimate voter who has followed the protocol, the composition of E’ and D'(V) will reveal V, and thus a vote for either Alice or Bob. Indeed, for any place in the two-dimensional array where E’ and D'(V) match up, it will be clear that a vote was cast and how it was cast. This vote will register either in Alice’s ledger of votes or Bob’s, and the mapping between the ballot ledger and the ledgers of counted votes will be clear.

This double uploading approach to ballots keeps the identity of the voters responsible for the ballots secure by having voters upload all their keys into one communal bin, as it were, and all the locks into another communal bin. It’s then up to the server to try all the keys on all the locks. Whenever a key opens a lock, a vote is cast. The slide handout accompanying this article visually clarifies how this lock-and-key approach works:

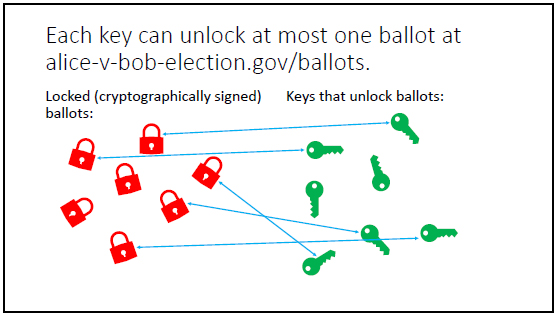
What’s particularly significant to the voter with this lock-and-key approach is that it allows the voter to track and verify how the voter’s actual ballot contributes a vote to the candidate of the voter’s choice. That’s because voters are able to identify their exact cryptographically signed ballots of the form D'(V) as well as their public keys E’ on the ledger of ballots — these will be clearly visible to the voters who uploaded them. This approach to trying all keys in all locks is eminently computable, with the computational complexity growing not just polynomially but even quadratically (thus very manageably) according to the size of the underlying computational problem. Elections with hundred of millions of voters can readily be handled with this approach.

5.10 An Important Asymmetry

In the Cryptosecure Election Protocol, an important asymmetry exists between, on the one hand, legitimate voters tracking their ballots and seeing that they are actually counted and, on the other hand, legitimate voters or other responsible third parties preventing bogus ballots from being counted. With the CEP, voters are easily able to confirm their own votes, but without the voter or party responsible for a vote available, it becomes more difficult to disconfirm a vote.

Here’s how this asymmetry plays out. For any cryptographically signed ballot of the form D'(V), a voter will want to confirm one of three things:

1. This is my ballot.
2. This isn’t my ballot.
3. This isn’t anybody’s ballot.

The CEP allows legitimate voters to track their ballots. A voter N who has uploaded D'(V) and E’ onto the ledger of ballots will be able to find those two items digitally represented there and will be able to confirm that they match up to contribute a vote to Alice’s or Bob’s ledger of received votes. That’s great for voters confirming their own votes, but not for voters or concerned third parties attempting to disconfirm the votes of others.

Because the CEP treats votes as belonging to voters, votes created out of thin air (i.e., ascribed to voters who don’t actually exist, or phantom voters, as we’ll call them) or votes ascribed to actual voters who are not voting or otherwise paying attention could conceivably slip through the cracks. A vote created in the name of a live actual voter by registering this voter under a fraudulent proof of identity and setting up public-private key pairs unknown to the actual voter can be redressed once the voter challenges the bogus information entered in the voter’s name on the ledger of registered voters (recall the 5-tuple array; the actual voter will insist that it be changed).

Provided that the ballot, cryptographically signed by D’, has yet to be uploaded, a bogus array in the ledger of registered voters can be invalidated by the real voter, thus removing (E,D) and (E’,D’) from any authorization for uploading a ballot onto the ledger of ballots. This means, however, that the registration period for updating the ledger of registered voters needs to be separate from and precede the actual voting period during which cryptographically signed ballots and their keys are uploaded (unlike presently, where in some states voting and registration periods overlap).

This restriction should not pose a problem, however, since the CEP allows all voting to occur online and without delays, so all votes could be readily cast and confirmed on a single day. But if the registration period and the voting period are allowed to overlap, bogus ballots submitted during that overlapping time period in the name of real voters will be impossible to recall by the real voters. It’s like showing up at a polling place and being informed that the record shows you have already voted. At that point, it’s probably too late.

Finally, the creation, on the ledger of registered voters, of identities of voters that don’t even exist poses a distinct problem for the CEP. Basically, bad actors are in this case simply manufacturing voters and votes. While it will be possible to confirm that these phantom voters voted, it will not be possible, within the CEP, to recall their votes once the ballots in their names are cast or to know who they voted for.

The only recourse in the CEP for dealing with such phantom voters is to rule them out, as much as possible, from the ledger of registered voters from the start. Given that the registration period of voters will, within the CEP, strictly precede the voting period, it will be up to concerned third parties, and ideally the election commission itself, to make the PoI for voters sufficiently stringent so that only real voters can get past the gatekeeping safeguards and onto the ledger of registered voters.

The bottom line is that security against phantom voters must occur and can only occur by securing the ledger of registered voters. To the degree that fraud here abounds, it may be necessary to unmask PoI information about questionable voters and even insist on direct contact with and confirmation from them.

This problem of phantom voters, however, can be mitigated even if it cannot be totally eliminated. A crucial step toward mitigation, besides stringent PoI requirements, will be instituting a lag between the registration period for voters (during which their PoI data is entered on the ledger of registered voters) and the voting period (during which cryptographically signed ballots and corresponding keys are uploaded).

If the registration period ends at twelve midnight and voting begins right after, it could be that hundreds of thousands of new phantom voters are suddenly created out of thin air at 11:59pm (thereby placing them on the ledger of registered voters just before the deadline) and then vote at 12:01am (thereby upload their cryptographically signed ballots and keys just after the deadline). Enforcing a lag will provide a period during which phantom voters can be identified and weeded out (and the fraudsters responsible hopefully brought to justice).

5.11 Loose Ends and Loopholes

The CEP has many moving parts and those parts need to be suitably coordinated. To the degree they are, I’m persuaded the CEP can be made to work, guaranteeing free and fair elections. But the devil will be in the details. Take, for instance, the concern about phantom voters in the last subsection. Imagine a legitimate good-faith voter named N uploads at alice-v-bob-election.gov/ballots/ballot-upload a cryptographically signed ballot D'(V) by first providing and verifying ownership of the ballot via the private-public key pair (E,D) per the CEP. What is to prevent a corrupt election commission from substituting for D'(V) another ballot and then down the line uploading the key that unlocks it, thereby removing N’s legitimate ballot and putting another in its place?

As it is, because uploaded ballots will be visible online, N will instantly see that the rightful ballot D'(V) was not in fact uploaded. N will thus have cause for redress. If the election commission, in the ledger of registered voters, marks N as having voted, then N can forcefully probe what happened to D'(V) and why it is not appearing on the ledger of ballots. Because hash(D’) is next to N’s name in the ledger of registered voters, N can even reveal D’, proving both that this key belongs to N and that no cryptographically signed ballot using that key appears on the ledger of ballots. Making such a case will be a hassle for N, however, and with a sufficiently corrupt election commission, delays and smokescreens may skew the outcome of the election before N’s vote gets properly counted.

This problem has another variant. A thoroughly corrupt election commission could simply start uploading multiple ballots of the form D'(V) and then also upload the corresponding keys, causing votes to be counted but at the same time not even bothering to put check marks next to names in the ledger of registered voters to signify that a voter has voted. The election commission would thus bypass the upload procedure for cryptographically signed ballots. This would lead to a math inconsistency in that no registered voters would have their names marked off as having voted, but new cryptographically signed ballots would nonetheless be appearing. An arithmetic inequality would thus exist between the number of supposed votes checked off on the ledger of registered voters and the number of cryptographically signed ballots appearing on the ledger of ballots.

To avoid such an obvious math error, a corrupt election commission will be strongly tempted to manufacture phantom voters in the ledger of registered voters. Their names can then be checked off as having voted while uploading ballots cryptographically signed in their names. This puts a security burden on the ledger of registered voters, to make sure that no such phantom voters reside there. We addressed this point and ways to mitigate it in the last section, but the challenge will be to keep this problem firmly in check.

A particularly problematic point with secret ballots, and this is a problem for all elections that attempt to keep the identity of voters separate from their ballots, is the handoff of the ballot from voter to the election commission. At the moment of handoff, strange and spooky things can happen. In the digital context, there’s always the prospect of someone attaching a tracking pixel to the ballot. But even in a paper context, distinguishing marks can be added to make clear which voter cast which ballot. Such marks don’t even need to exactly identify a given voter. A paper ballot could have a seemingly stray mark if a voter is thought to belong to one party, another stray mark if a voter is thought to belong to another party. And perhaps ballots with the “wrong” stray mark will simply disappear.

I knew a professor who at the end of the term would hand out long student evaluations that required multiple sheets of paper. The professor would staple the sheets in different ways and give them accordingly to different students or groups of students. He could even use a unique staple location and orientation if he really wanted to know what one particular student was thinking about him. The point is that there are always ways to track information that is transmitted in a causal chain. Safeguards and penalties can help. Privacy statements on websites now carry liabilities if the websites don’t adhere to the terms of those statements.

Yet even without such shenanigans, there can be indirect ways to track voters and connect them to their ballots. Suppose voter N first proves his or her identity by means of the private-public key (E,D) and then uploads the cryptographically signed ballot D'(V). At the same time, the election commission marks N as having voted on the ledger of registered voters. Two events now are happening within a narrow window of time: N being shown to have voted on the ledger of registered voters and D'(V) appearing on the ledger of ballots. If few votes are cast at the time, temporal proximity may be enough to connect N with D'(V), thus undermining the secrecy of the ballot. It might therefore be best not to put a check mark next to a voter’s name right after he or she votes but to wait for a larger block of voters to have voted and then to mark all their names at the same time as having voted.

Like most cryptographic protocols, the CEP invites an arms race in which bad actors try to subvert it and good actors try to shore it up. Especially important will be decentralized safeguards. For instance, in addition to the use of data integrity methods, it will help to have independent third parties acting as poll monitors. A poll monitoring organization, for instance, could run a mirror site to alice-v-bob-election.gov so that whenever a voter N uses (E,D) to upload the cryptographically signed ballot D'(V), (E,D) is also used on the mirror site to upload D'(V). The same privacy restrictions would then have to apply to the poll monitoring organization as to the election commission so that it can’t publicly identify N, or any information that could be used to identify N, through the uploads.

The bottom line is that a successfully executed CEP will require careful consideration of what could go wrong as well as what needs to go right with it. A successful implementation of the CEP means understanding what bad actors might do to subvert it (thus committing election fraud), and what good actors need to do to keep it from being subverted (thus ensuring a free and fair election).

5.12 The Cryptosecure Election Protocol in a Nutshell

That’s the Cryptosecure Election Protocol. In a nutshell, it requires a server, such as alice-v-bob-election.gov, and then four ledgers or subdirectories (five if you count the ledger of eligible voters):

1. alice-v-bob-election.gov/alice
2. alice-v-bob-election.gov/bob
3. alice-v-bob-election.gov/registered-voters
4. alice-v-bob-election.gov/ballots

All four ledgers will be publicly viewable and tracked in real time with data integrity methods to ensure that no unwarranted changes are made. The ledger of registered voters comprises 5-tuples of the form <N, hash(Z), encrypt(Z), E, hash(D’)> (becoming 6-tuples when a vote is counted), with underlying proof of identity Z for N and two public-private key pairs (E,D) and (E’,D’), the private keys being known only to N.

When N writes up a ballot V that votes for either Alice or Bob, N uses E to authorize uploading D'(V), thus marking on the ledger of registered voters that N has cast a vote. And then, anonymously, N uploads E’. The uploads are then both visible at alice-v-bob-election.gov/ballots. Phantom voters can try to co-opt this approach to uploading ballots, so they must be stopped before it gets to that point by introducing strong protections against bogus proofs of identity and by introducing a lag between the time of voter registration and the time of actual voting.

Even though many locks and many keys will be uploaded onto the ledger of ballots, only one lock and one key can ever work together. When there is a fit, a vote is cast, mapped onto either Alice’s ledger or Bob’s. At each step, the voter knows exactly how the information and data he or she has inputted is being used and how it contributes or fails to contribute a vote to a candidate, all the while keeping the voter’s identity confidential.

Finally, even though the steps outlined here might seem daunting, in fact a single app could easily handle all the hash functions, QR barcodes, public-private key combinations, nonces, etc. described in the Cryptosecure Election Protocol, basically handling all the grunge work involved with proof of identity and uploading all crucial data.

Such apps, by simply following the protocol, can be multiply realized, with different companies providing the same functionality so that voters are not at the mercy of any one app development company. Most importantly, through the Cryptosecure Election Protocol, voters will be able to track their votes, see that they have been correctly counted, and be able to provide rock-ribbed evidence to the contrary if there is election fraud.

***

Note that a simplified slide visualization of the CEP is available here as a pdf: “How a Crypto Protocol Can Ensure Free and Fair Elections.”